Recall Maxwell's equations:
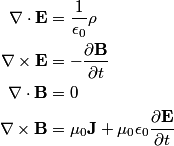 If you plug the given electric field into Gauss's Law, you will find that 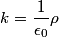 We are told that 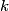 is a nonzero constant. Therefore, is a nonzero constant. Therefore, 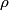 must also be nonzero, and so there must be charge density in the region. Therefore, answer (B) is correct. must also be nonzero, and so there must be charge density in the region. Therefore, answer (B) is correct. |